Parabolic Reflectors

Parabolic Reflecting Antennas

Composition by N8PPQ

Recent commercialization of the microwave spectrum by the telecommunication and satellite TV industries has introduced to the landscape an engaging new crop of antennas. This paper is intended to present information fundamental to the understanding of the geometry of these high-tech blossoms.

A "dish" antenna has the optimum form for collecting electromagnetic radiation and bringing it to a focus. The reflecting surface is based on a three-dimensional shape called a paraboloid, and has the unique property of directing 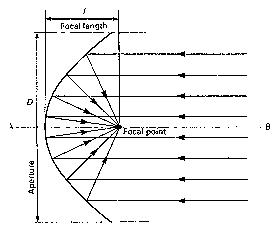all incoming wave fronts prependicular to its axis, in phase, to a point focus. Reflective antennas are generally made of steel, aluminum, or fiberglass with an embedded reflective foil.

The location of the focal point is a property of the geometry of the dish and is independent of the radiation wavelength. The diagram here shows the basic configuration and identifies the focal point, focal length, and aperture.

The paraboloid is defined as the set of points equidistant from a fixed point (the focus) and a plane, (the directrix). It is straight forward to show that this geometric configuration can work for our purpose. The diagram below illustrates the process involved.

Electromagnetic energy radiating from an omni-directional source consist of spherical waves of increasing radius. At great distances these are approximated by planar fronts and are called plane waves. We see that plane waves coming from the left are reformed after reflection into converging spherical waves. In order for the plane waves to ultimately converge on some point F, the path lengths for all parts of the waves must be equal. In the center of the diagram above we have two arbitrary points A1 and A2, on the surface of the reflector. We envision two points riding on a wave crest and tracing out rays which describe their path. For rays parallel to the axis of the paraboloid and incident to A1 and A2, we have

Path Length = W1A1 + A1F = W2A2 + A2F (*)

Since the plane waves are parallel to the plane Sigma, we have,

W1A1 + A1D1 = W2A2 + A2D1.

We see that (*) will be satisfied for a reflecting surface where AF = AD for any point A on the surface. It is clear by the definition that the surface is a paraboloid with F as its focus and Sigma as its directrix.

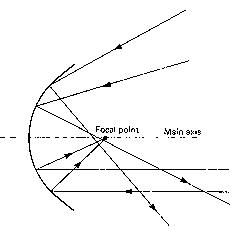The parabolic reflector is very effective at rejecting unwanted signals and electrical "noise". As the diagram to the left illustrates, waves which enter at angles other than parallel to the main axis are reflected so as to miss the focal point altogether. There is a "head unit" (also called a "feed horn") placed at the focal point of the antenna. It is said to illuminate the dish; a term is used even if the antenna is designed for reception only, (since reception is basically the reverse process of transmission, descriptions of antenna theory seem to switch, at a whim, between transmission and reception terminology).

The above argument was intuitive, but not totally convincing, (do you see why?). I have a couple Maple programs for you to enjoy - you can make your own reflecting antenna systems and watch the rays bounce to a focus, just like we claim they should - but this is still a formational type reasoning. Sophisticated math scolars will expect a formal, analytical proof about now. Please click here to view said proof. I am rather proud of it. Or click below to bypass it.

Proof Bypass