N8PPQ

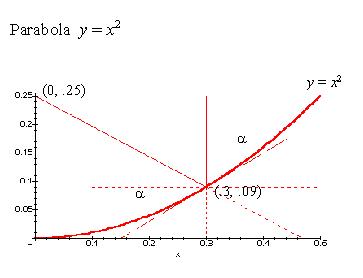
Here is a proof that any paraboloid will work as a reflecting antenna, focusing incoming rays which are parallel to the axis of symmetry to a point. I have included Maple plots of a particular parabola, 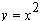 , but the proof embraces all parabolas. The plots will be helpful in visualizing our plan of attack.

We see below that a certain incoming vertical ray, 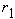 , impinges upon the parabola at the point ( 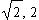) and forms an angle, 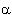, with the line tangent to the curve at the point of incidence. The reflected ray is 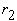 . We will assume that the angle of reflection is equal in measure to the angle of incidence. This is a sound assumption but, more to the point, it has nothing to do with paraboloids and so does not detract from the value of this proof. We have indicated this congruence in the diagram below.

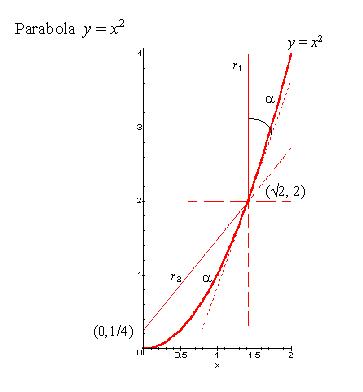
Our task is to show that ray 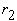 proceeds from the point of reflection to the parabolas' focus. It is not enough for us to simply demonstrate this truth for a set of selected incoming rays and a selection of parabolas, which is what we did with our Maple program. The diagram above is such an illustrative example, showing a particular ray striking a particular point on a particular parabola. Our proof must apply to all incoming rays parallel to the axis of symmetry and all parabolas. The proof is straightforward.

We begin with the formula for a vertically orientated parabola with its vertex on the origin, without derivation:

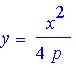
Here p is the location of the focus. We note that an incident ray strikes the parabola at a point we call (x, y). The slope of the parabola at that point is the derivative

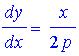
From trigonometry we know that

,

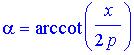and that the slope of 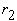 is

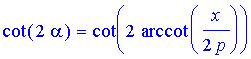
(invoking the vertical angle theorem). This is true if the ray strikes above the focus, as in the first diagram, or below it, as illustrated here.

We want to show that a ray drawn from point (x, y) with slope cot(2*arccot(x/2p)) will intersect point (0, p). Ohhkkaaayyyy...

Note that the slope of a line passing through (x, y) and (0, p) can be expressed as the familiar "rise over run" ratio:

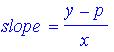
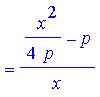
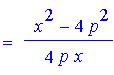
For our ray, 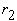 , to include point p, these two expressions for the slope must be equal. So our proof will be complete if we can show that

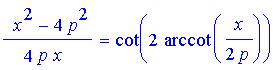
We decide to work on the right side of this conjecture to reduce it to the expression on the left. But first, we utilize Maple to plot both functions of x in order to check our logic.

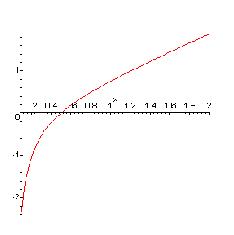
Both functions produced the same plot (above). This encouragement was key to my quick success: it gave me confidence, (I love Maple).

We will rely on the following identities:

(1) cot(x) = 1/tan(x),

(2) tan(2x) = 2*tan(x)/(1 - tan^2(x)),

Beginning with our trigonometric expression for the slope of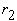 

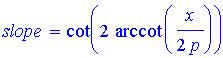
we utilize (1) and (2) to obtain

.

Expanding and applying (1) we have

which reduces immediately to

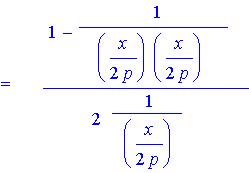
and

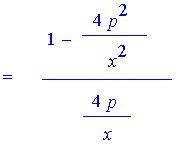A little algebra yields

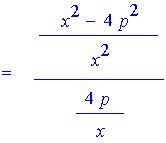
and finally

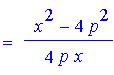
as we hoped. We have shown that a ray drawn from point (x, y) with slope cot(2*arccot(x/2p)) will intersect point (0, p). Hence, any paraboloid will work as a reflecting antenna, focusing incoming rays parallel to the axis of symmetry, to a point. QED 

Click here for more information on parabolic reflectors