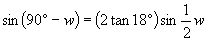
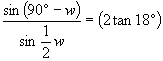
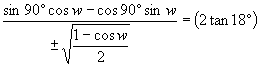
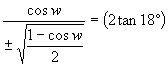
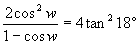
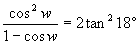
|
I was surprised to see the R's cancel,
but of course
they should. The central
angles are not related to the radius.
Now we
invoke the identies: 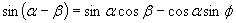 and and
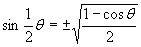 .
.
Now sin 90º = 1, of course, and cos 90º =
0.
Now square both sides to get rid of the
radical.
We'll have to check our
results for extraneous solutions.
I looked at
this for a while. I expected the Pythagorean identity to help,
i.e.
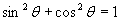 , hence , hence
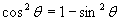 ,
which factors thus: ,
which factors thus:
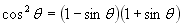 , neither of
which cancels the denominator. , neither of
which cancels the denominator.
|