Preliminaries:

I would like to tie this experiment in with others that deal with pendulums in some way. Double pendulums, rotating pendulums (where the bob hangs straight and rotates), and the Foucault pendulum are things I'd like to consider.

Prelab Questions:

1) True/False: A pendulum oscillates back and fourth with the same period of time, for any angle of swing less than 90°. (Explain your answer.)

2) True/False: A pendulum oscillates back and fourth with the same period of time, regardless of the mass of its swinging bob. (Explain your answer.)

3) Sketch a free-body diagram of a pendulum at two critical instants: where the bob has its maximum and minimum kinetic energies.

____________________________________________

Physics ### lab

Simple Harmonic Motion - The Pendulum

Purpose: The purpose of this experiment is to study the swinging pendulum.

Equipment: For this experiment, you will need:

* Pendulum apparatus with interchangeable weights and rods.

* Stopwatch.

* Protractor

Background:

Below, you can see a free-body diagram of a pendulum at some displacement q.

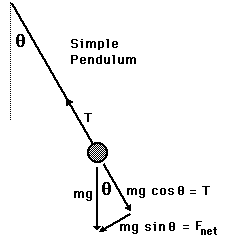
We denote the bob's mass m and will call the rod length L.

In this position, the pendulum experiences a net restoring force due to gravity:

F_r = - mg sinq.

For small angles, sin q $\approx$ q. (q is expressed in radians). The negative sign above means that the force opposes a displacement.

Since arc lengths are related to radian measure by S = rq, we have:

So, for small displacements, the restoring force can be written:

Since the restoring force is proportional to the displacement, the pendulum is a simple harmonic oscillator with ``spring constant'' k = mg/L . The period of a simple pendulum is therefore:

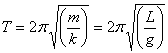
So, at small angles, the amplitude of the pendulum has practically no effect on the period. This is what makes pendulums such good timekeepers. As they inevitably lose energy due to frictional forces, their amplitude decreases, but the period remains constant.

Of course, this approximation does not work for larger angles.

Procedure:

1) Install the heavy bob on the long rod. Measure the weight and the length of the rod. Record your measurements.

2) Release the bob from an angle of about 2°. Record the time it takes for five full swings. Divide by five to get an average time for the period of oscillation. Record this time period.

3) Predict how the period will change if you release the bob from 20°. Record your prediction. Include an explanation of your reasoning.

4) Release the bob from an angle of about 20°. Record the time it takes for five full swings. Divide by five to get an average time for the period of oscillation. Record this time period.

5) How does your observation compare to your prediction?

6) Predict how the period will change if you release the bob from 80°. Record your prediction. Include an explanation of your reasoning.

7) Release the bob from an angle of about 80°. Record the time it takes for five full swings. Divide by five to get an average time for the period of oscillation. Record this time period.

8) How does your observation compare to your prediction?

9) Predict how the period will change if you decrease the bob weight by half. Record your prediction. Include an explanation of your reasoning.

10) Release the bob from an angle of about 20°, with a bob weight about half the original. Record the time it takes for five full swings. Divide by five to get an average time for the period of oscillation. Record this time period.

11) How does your observation compare to your prediction?

12) Predict how the period will change if you decrease the rod length by half. Record your prediction. Include an explanation of your reasoning.

13) Release the bob from an angle of about 20°, with a rod length about half the original. Record the time it takes for five full swings. Divide by five to get an average time for the period of oscillation. Record this time period.

14) How does your observation compare to your prediction?

Follow up Questions for Students:

1) What kind of error would be introduced to the calculation of period, T, if we used the small angle approximation where q = 80°?

2) Two flywheels with different moments of inertia will accelerate at different rates under the influence of identical forces. Why is it that the pendulum period is the same regardless of the mass of the bob?

3) How is it that the pendulum in a clock does not power down to a standstill? (I'm looking for damped and driven harmonic motion.)

__________________________________

Comments

I'll show the apparatus I used for this experiment. It's quite large. However, it could easily be scaled down to a desktop model.

I started out by making some bobs. I figured that if they were heavy, friction wouldn't be a problem. I didn't want to take the time to incorporate bearings, although I plan to, if I ever use this setup again. I wanted to use wire instead of a string, in case the bob went above 90°.

The big bob is 5-1/2 pounds. The other one is about half that weight. The little one is much smaller. I didn't even weigh it. The rod is 3/16 D. I had one 40" long and another one 80" long. I started off swinging the five-pounder on the long rod at 20° and we timed the period. Then we tried about 3°. It rocked forever, but I had the class count only five reps and averaged them.

Then, I raised the bob over my head and asked them to predict the period, as compared to the others. (You can't see the built-in glass case to the right, or the roller cart full of laptop computers in front of it.)

It worked fine. It was quite solid. We counted five full swings (starting from the far right). After that, we tried the smaller weight, (on the floor in front). Then we shortened the rod and tried again.

We see that for small angles, (q << 1), the system behaves like a simple harmonic oscillator.

After all that, we made double pendulums with different weights and rods. They are real cool. Below, you can't see the smallest weight because it's blurred out. It's moving real fast. That weight hangs on a 1/8" rod. I used wire nuts to hold the thing on because it got chaotic real quick. Actually, what I was demonstrating was "chaotic motion", (in the technical sense).

Below is a graphic representation of the kind of motion exhibited by the double pendulum above.

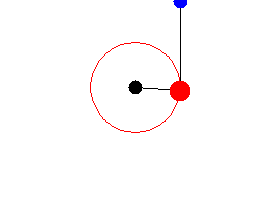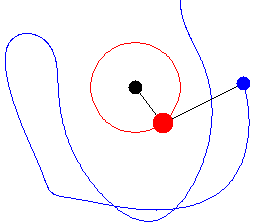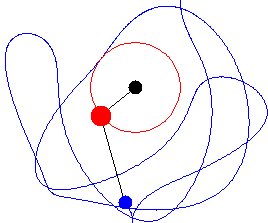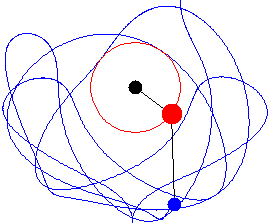
Sources

pend.html

Simple Pendulum

http://hyperphysics.phy-astr.gsu.edu/hbase/pend.html#c1

Double Pendulum

http://scienceworld.wolfram.com/physics/DoublePendulum.html

The Simple Pendulum

http://theory.uwinnipeg.ca/physics/shm/node5.html